Data Structure Summary

Linked List

LinkedList − A Linked List contains the connection link to the first link called First and to the last link called Last.

Singly Linked List
 A singly linked list is a set of nodes where each node has two fields ‘data’ and ‘link’. The ‘data’ field stores actual piece of information and ‘link’ field is used to point to next node.

Doubly Linked List
A doubly linked list contains an extra pointer, typically called previous pointer, together with next pointer and data which are there in singly linked list.


Difference between Singly linked list and Doubly linked list

In SingleLinkList, the traversal can be done using the next node link only.In DoublyLinkList, the traversal can be done using the previous node link or the next node link.
The SingleLinkList occupies less memory than DoublyLinkList as it has only 2 fields.The DoublyLinkList occupies more memory than SingleLinkList as it has 3 fields.
Less efficient access to elements.More efficient access to elements.

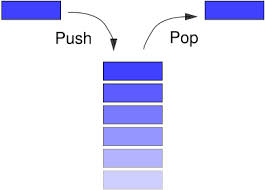
Stack
A stack is a linear data structure in which elements can be inserted and deleted only from one side of the list, called the top. A stack follows the LIFO (Last In First Out) principle. The insertion of an element into stack is called push operation, and deletion of an element from the stack is called pop operation. In stack we always keep track of the last element present in the list with a pointer called top.



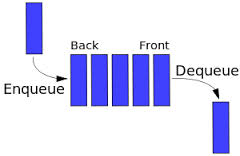
Queue
A queue is a linear data structure in which elements can be inserted only from one side of the list called rear, and the elements can be deleted only from the other side called the front. The queue data structure follows the FIFO (First In First Out) principle, i.e. the element inserted at first in the list, is the first element to be removed from the list. The insertion of an element in a queue is called an enqueue operation and the deletion of an element is called a dequeue operation.



Expression Parsing

Infix Notation

We write expression in infix notation, a - b + c, where operators are used in-between operands. It is easy for us humans to read, write, and speak in infix notation but the same does not go well with computing devices. An algorithm to process infix notation could be difficult and costly in terms of time and space consumption.

Prefix Notation

In this notation, operator is prefixed to operands,operator is written ahead of operands. For example, +ab. This is equivalent to its infix notation a + b. Prefix notation is also known as Polish Notation.

Postfix Notation

This notation style is known as Reversed Polish Notation. In this notation style, the operator is postfixed to the operands, the operator is written after the operands. For example, ab+. This is equivalent to its infix notation a + b.

Hashing

Hashing is a technique to convert a range of key values into a range of indexes of an array.

In hashing, large keys are converted into small keys by using hash functions. The values are then stored in a data structure called hash table.

Hash Table
   Hash table is a data structure that represents data in the form of key-value pairs. Each key is mapped to a value in the hash table. The keys are used for indexing the values/data. A similar approach is applied by an associative array.

Basic Operations

Following are the basic primary operations of a hash table.
  • Search − Searches an element in a hash table.
  • Insert − inserts an element in a hash table.
  • delete − Deletes an element from a hash table.

Binary Tree
 Binary trees can have at most two children for each parent. Every node contains a 'left' reference, a 'right' reference, and a data element. The topmost node in the tree is called the root node. Nodes with children are parent nodes, and the child nodes contain references to their parents. A node with no children is called a leaf node.
Different Types of Binary Tree with colourful illustrations

Full Binary Tree

Full Binary Tree is a Binary Tree in which every node has 0 or 2 children.

Complete Binary Tree

Complete Binary Tree has all levels completely filled with nodes except the last level and in the last level, all the nodes are as left side as possible.

Perfect Binary Tree

Perfect Binary Tree is a Binary Tree in which all internal nodes have 2 children and all the leaf nodes are at the same depth or same level.

Balanced Binary Tree

Balanced Binary Tree is a Binary tree in which height of the left and the right sub-trees of every node may differ by at most 1.

Comments

Post a Comment

Popular posts from this blog

AVL Tree & B Tree

Image
AVL Tree AVL tree is a self-balancing binary search tree in which each node maintains an extra information called as balance factor whose value is either -1, 0 or +1. AVL tree got its name after its inventor Georgy Adelson-Velsky and Landis. Balance Factor Balance factor of a node in an AVL tree is the difference between the height of the left subtree and that of right subtree of that node. Balance Factor = (Height of Left Subtree - Height of Right Subtree) or (Height of Right Subtree - Height of Left Subtree) The self balancing property of an avl tree is maintained by the balance factor. The value of balance factor should always be -1, 0 or +1. AVL Rotations Left Rotation If a tree becomes unbalanced, when a node is inserted into the right subtree of the right subtree, then we perform a single left rotation Right Rotation AVL tree may become unbalanced, if a node is inserted in the left subtree of the left subtree. The tree then needs a right
Read more

Binary Tree

Image
A binary tree is made of nodes, where each node contains a "left" pointer, a "right" pointer, and a data element. The "root" pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller "subtrees" on either side. A null pointer represents a binary tree with no elements -- the empty tree. The formal recursive definition is: a  binary tree  is either empty (represented by a null pointer), or is made of a single node, where the left and right pointers (recursive definition ahead) each point to a  binary tree .        A "binary search tree" (BST) or "ordered binary tree" is a type of binary tree where the nodes are arranged in order: for each node, all elements in its left subtree are less-or-equal to the node (<=), and all the elements in its right subtree are greater than the node (>).  Types of binary tree A  full binary tree  which is also called as
Read more