AVL Tree & B Tree

AVL Tree

AVL tree is a self-balancing binary search tree in which each node maintains an extra information called as balance factor whose value is either -1, 0 or +1.

AVL tree got its name after its inventor Georgy Adelson-Velsky and Landis.

Balance Factor

Balance factor of a node in an AVL tree is the difference between the height of the left subtree and that of right subtree of that node.

Balance Factor = (Height of Left Subtree - Height of Right Subtree) or (Height of Right Subtree - Height of Left Subtree)

The self balancing property of an avl tree is maintained by the balance factor. The value of balance factor should always be -1, 0 or +1.

AVL Rotations

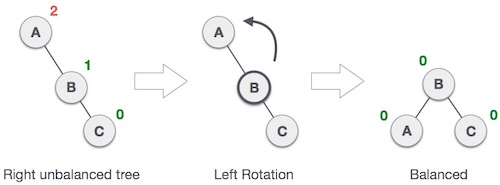
Left Rotation

If a tree becomes unbalanced, when a node is inserted into the right subtree of the right subtree, then we perform a single left rotation

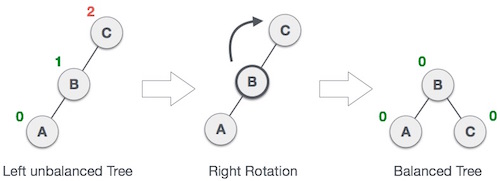
Right Rotation

AVL tree may become unbalanced, if a node is inserted in the left subtree of the left subtree. The tree then needs a right rotation.

Left-Right Rotation

Double rotations are slightly complex version of already explained versions of rotations. To understand them better, we should take note of each action performed while rotation. Let's first check how to perform Left-Right rotation. A left-right rotation is a combination of left rotation followed by right rotation.

Right-Left Rotation

The second type of double rotation is Right-Left Rotation. It is a combination of right rotation followed by left rotation.

AVL TREE SIMULATION

INSERT 5,6,7,0,4,3,8

DELETE 3,4,8

B Tree

B-Tree is a self-balancing search tree.B Tree is a specialized m-way tree that can be widely used for disk access. A B-Tree of order m can have at most m-1 keys and m children. One of the main reason of using B tree is its capability to store large number of keys in a single node and large key values by keeping the height of the tree relatively small.

To understand the use of B-Trees, we must think of the huge amount of data that cannot fit in main memory. When the number of keys is high, the data is read from disk in the form of blocks. Disk access time is very high compared to main memory access time. The main idea of using B-Trees is to reduce the number of disk accesses.

Properties

B-Tree contains the following properties.

Every node in a B-Tree contains at most m children.

Every node in a B-Tree except the root node and the leaf node contain at least m/2 children.

The root nodes must have at least 2 nodes.

All leaf nodes must be at the same level.

Search

Search is similar to the search in Binary Search Tree. Let the key to be searched be k. We start from the root and recursively traverse down. For every visited non-leaf node, if the node has the key, we simply return the node. Otherwise, we recur down to the appropriate child (The child which is just before the first greater key) of the node. If we reach a leaf node and don’t find k in the leaf node, we return NULL.

Insert

As in insertion, we must make sure the deletion doesn’t violate the B-tree properties. Just as we had to ensure that a node didn’t get too big due to insertion, we must ensure that a node doesn’t get too small during deletion (except that the root is allowed to have fewer than the minimum number t-1 of keys). Just as a simple insertion algorithm might have to back up if a node on the path to where the key was to be inserted was full, a simple approach to deletion might have to back up if a node (other than the root) along the path to where the key is to be deleted has the minimum number of keys.

Delete

Delete The deletion procedure deletes the key k from the subtree rooted at x. This procedure guarantees that whenever it calls itself recursively on a node x, the number of keys in x is at least the minimum degree t . Note that this condition requires one more key than the minimum required by the usual B-tree conditions, so that sometimes a key may have to be moved into a child node before recursion descends to that child. This strengthened condition allows us to delete a key from the tree in one downward pass without having to “back up” (with one exception, which we’ll explain). You should interpret the following specification for deletion from a B-tree with the understanding that if the root node x ever becomes an internal node having no keys (this situation can occur in cases 2c and 3b then we delete x, and x’s only child x.c1 becomes the new root of the tree, decreasing the height of the tree by one and preserving the property that the root of the tree contains at least one key (unless the tree is empty).